Domar el gerrymander con la búsqueda geoespacial

Conceptos básicos

Antes de seguir leyendo, tómese unos minutos y lea el excelente post sobre búsqueda geoespacial en Couchbase, publicado por mi amigo y colega Brian Kane: https://www.couchbase.com/blog/geospatial-search-how-do-i-use-thee-let-me-count-the-ways/

Adelante; esperaré.

Ahora que has vuelto, sabrás que una forma estupenda de aprovechar el motor de búsqueda de texto completo de Couchbase es pasarle una serie de vértices que identifiquen un polígono (normalmente irregular) que describa una región geográfica. El ejemplo de Brian utiliza diez pares de puntos lat/long:

Estos puntos delimitan aproximadamente una región de Tennessee, al sur de la autopista, al norte del límite del Parque Nacional y dentro de un único condado... suficientemente bueno para el análisis requerido, y fácil de pegar en tu solicitud. Teniendo esto en cuenta, el motor de índice de búsqueda de texto completo (FTS) de Couchbase puede devolver fácilmente todos los elementos de datos necesarios asociados con puntos dentro (o fuera) del perímetro. (Brian da un gran ejemplo de esto en su post).

La llave inglesa (o quizá, el distrito con forma de llave inglesa)

Pero, ¿y si su región poligonal es extremadamente detallada y compleja, y requiere tal vez miles de pares de puntos lat/long para describirla? ¿Disponemos de ejemplos de este tipo? Sí. Gracias a la ardua labor de las legislaturas de los cincuenta estados y/o sus sustitutos, tenemos muchos ejemplos de regiones de este tipo en forma de distritos del Congreso de los Estados Unidos. Y gracias a Couchbase N1QL y a la búsqueda geoespacial FTS, tenemos los medios para gestionar los datos con facilidad.

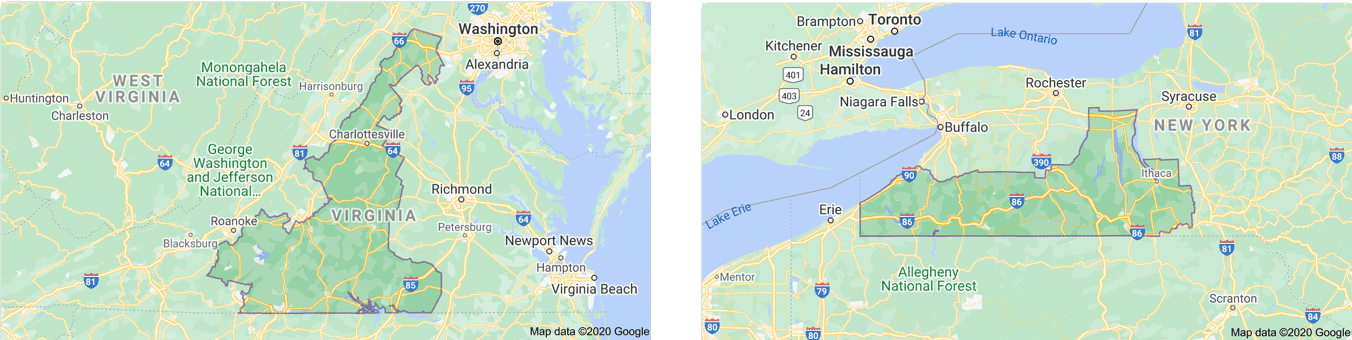
El distrito medio del Congreso de EE.UU. requiere 8.694 vértices para definirse. Esto se debe a razones prácticas (se espera que todos los distritos tengan aproximadamente el mismo número de ciudadanos), políticas (los partidos en el poder pueden deformar los límites de los distritos para que los votantes los mantengan así, lo que se denomina "gerrymandering") y geográficas (muchos de ellos se basan en parte en ríos, lagos, costas oceánicas, montañas y otros límites naturales). El distrito geográficamente más complejo (es decir, el que requiere el mayor número de vértices para ser descrito) es el 5º distrito electoral de Virginia, que necesita la friolera de 40.145 pares de latitud y longitud para ser descrito (y parece un T. Rex rampante al revés). El más sencillo, que sólo requiere 422, es el 36º Distrito Electoral de Nueva York, que parece un submarino escabulléndose del lago Erie.

Los datos

Claramente, entonces, vamos a querer almacenar y recuperar nuestros puntos geográficos de una base de datos si queremos implementar consultas contra ellos a gran escala. Y debido a que los puntos se encuentran probablemente en forma de una matriz incrustada, un documento JSON en Couchbase es justo el billete. Abajo hay un ejemplo de tal documento:

¿Por qué los datos tienen esta forma, te preguntarás, con los puntos del polígono incrustados en un array de un solo elemento sin nombre, incrustado en otro de "coordenadas", incrustado en un objeto de "geometría"? La respuesta sencilla es que a veces simplemente se trabaja con los datos que se tienen. (Se basa en la fuente pública que pude encontrar, una que era notablemente fácil de importar a Couchbase. Tal vez escriba un post aparte describiendo ese proceso). Y aunque los datos son un poco engorrosos, el lenguaje N1QL, como veremos más adelante, facilita la recuperación de lo que necesitamos.

El otro conjunto de datos que nos ocupa constituye la parte principal de nuestro ejemplo. Se trata de una lista de millones de votantes registrados (no te preocupes, he falsificado los nombres y las direcciones), junto con la afiliación a un partido y el historial de voto de cada uno. Un documento de muestra tiene este aspecto:

Caso práctico y configuración

Por último, nuestro caso práctico: Dado un elector individual por teléfono, ¿cómo puede un miembro del Congreso determinar rápidamente si la persona es o no miembro de su distrito electoral? Resolveremos el problema con FTS y N1QL.

Primero debemos preparar el índice FTS. En nuestro caso, indexaremos todos los documentos en función del campo de tipo Tipo. Indexaremos el Nombre como palabra clave, y el campo Geo como geopunto. Esto es lo que se ve en mi consola:

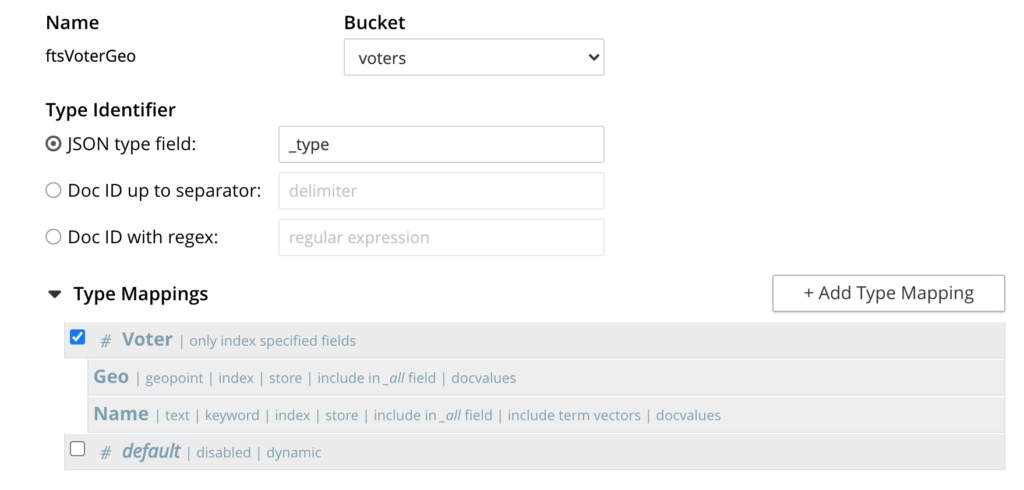
(El post de Brian profundiza en los pasos a seguir para construir un índice).

Una vez construido este índice, podremos pasarle una serie de puntos poligonales y recibir una serie de aciertos. Siguiendo el ejemplo de Brian, he probado esto usando un curl:

Esto me demuestra que una búsqueda en una simple región poligonal puede devolver y devolverá una lista de nombres. En teoría, podríamos detenernos ahí y dejar que la aplicación (o incluso el usuario) buscara entre los resultados para ver si encuentra el nombre del votante en cuestión. Pero podemos hacerlo mejor. Dejemos que el motor de búsqueda acote la búsqueda. Lo haremos mediante una búsqueda "conjunta". (Piense en un conjunto como un AND lógico y un disyunto como un OR lógico). A continuación se muestra el ejemplo de curl:

Puedes leer esto como "Si el geopunto está dentro de los límites del polígono y el nombre coincide con el nombre del votante, devuelve el acierto". Funciona a las mil maravillas, así que sabemos que nuestro índice FTS está correctamente definido.

La extracción

Ahora tenemos que probar la recuperación de los límites de un distrito individual de la base de datos. El primer paso consiste en una simple inspección de los datos que vamos a utilizar, quizá de un solo distrito:

Esto devuelve un resultado como este:

...y así sucesivamente durante otros 1,3 MB de un conjunto de resultados. No es de extrañar que no queramos cortar y pegar esto.

Nuestro objetivo, recuerda, es acabar con algo parecido a esto:

Así es como acabamos:

Esto es un trabalenguas, así que vamos a desentrañarlo. Recuerde que estamos trabajando con los datos que tenemos, en lugar de lo que idealmente podríamos querer, y los puntos del polígono que estamos buscando están incrustados en una matriz de un solo elemento sin nombre, incrustado en otro de "coordenadas", incrustado en un objeto de "geometría". Tenemos que desenrollarlos uno a uno. En primer lugar, vamos a eliminar la envoltura de la matriz sin nombre. Para ello, basta con solicitar que sólo se devuelva el único (primer o "zeroth") miembro de la matriz:

El objeto JSON devuelto por esta consulta tiene el siguiente aspecto:

Podemos convertirlo en un array (en lugar de un objeto JSON) utilizando select value:

Ahora tenemos el array muy grande que buscamos, aún envuelto en el único elemento de otro array:

Seleccionemos de ese conjunto de devoluciones:

Esto da lugar a un montón de pequeños objetos que podemos plegar a nuestra voluntad:

Ahora que podemos abordarlos vamos a convertir los tipos y realizar nuestra concatenación:

Los objetos resultantes tienen este aspecto:

Ahora usa select value para recibirlos como un array:

Y tenemos los resultados que buscábamos:

La facilidad de los CTE

El último truco que nos queda es un buen truco. Necesitamos una forma de referenciar el array que contiene los geopuntos como componente de una sentencia SQL más amplia. Afortunadamente, N1QL nos proporciona los medios para hacerlo en forma de Expresiones de Tabla Comunes (CTE). Las CTE, que se añaden a una consulta mediante la función con se evalúan una vez por bloque de consulta y pueden introducirse antes de una selección. Esto es exactamente lo que buscamos:

Ahora tenemos acceso a un conjunto de retorno evaluado "geopuntos" al que se puede hacer referencia en posteriores (o múltiples posteriores) sentencias SQL. Perfecto. Aquí se utiliza en la consulta final:

Aquí está: Un sencillo bloque de código de una sola pantalla que recupera los límites complejos de un distrito y los aprovecha como parte de una búsqueda geoespacial impulsada por N1QL. Pruebe esta técnica y supere sus propios retos geográficos.

Muchas gracias a Brian Kane por su post original y a Dmitry Lychagin por su ayuda para desentrañar las matrices anidadas.